Últimamente se ha venido exponiendo y aplicando en las
organizaciones, las Cadenas de Markov las cuales son ciertos modelos
estocásticos utilizadas comúnmente en el campo de la investigación de
operaciones que nos permiten analizar problemas de corto y largo plazo a
los que se les quiere saber su comportamiento futuro, con la condición de que
solamente el estado anterior a éste y de ningún otro más es el que importa.
Entre las aplicaciones de procesos markovianos en el
ámbito de la salud encontramos los siguientes casos:
ü -Permite medir el efecto
económico que provoca el uso de una determinada droga en la permanencia de un
paciente con cierto síndrome en una unidad de cuidado intensivo.
ü -Proporciona estudios
predictivos y comparativos (sexo y edades).
ü -Posibilita tomar decisiones
óptimas en la admisión de pacientes en una unidad específica.
ü -Nos permite realizar
descripciones de las evoluciones del paciente.
En
el caso que mostraremos a continuación, se predijo la duración promedio
de permanencia de un paciente en la UCI del hospital Dr. Luis Calvo Mackenna y
su evolución (ya sea positiva o negativa) a través de los diferentes niveles de
gravedad (estable, crítico, emergencia, etc) que se presentan ocasionalmente. A
continuación describiremos algunos detalles de la aplicación de las cadenas de
Markov cuyo conocimiento se espera
contribuya posteriormente a la gestión de dicha unidad de salud y los
resultados alcanzados.
MÉTODOS
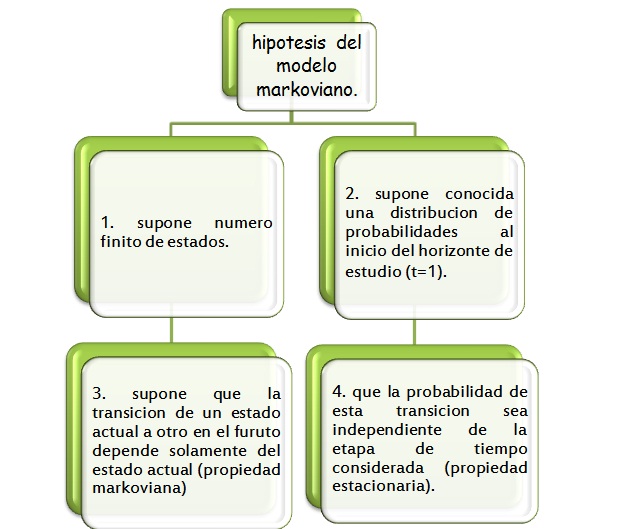
Una
cadena de Markov corresponde a una clase específica de proceso estocástico en
el ámbito de modelos probabilísticos.
Que representa el nivel
de gravedad a través del tiempo.
A
medida que transcurre el tiempo, los cambios de estado tienen lugar en términos
probabilísticos y son representados a través de las denominadas probabilidades
de transición entre estados, que en el caso de las transiciones en una etapa
corresponde a la probabilidad de pasar de un estado a otro desde una etapa de
tiempo t a la siguiente t+1.
Para
definir los estados de la cadena se empleara in determinado índice o score,
asociado a un nivel de riesgo y gravedad de un paciente de la UCIC. Para
determinar este score se toman en cuenta 6 factores:
Nota:
el rango no es el mismo para cada factor, pues permite establecer diferencias
relativas entre los distintos aspectos considerados.
La
importancia relativa entre los distintos factores se consigue definiendo un
score máximo que cambia con la importancia del factor considerado, el score
máximo para la edad es 8, para una cirugía previa es 8, para la condición
inicial es 12, para las complicaciones post-operatorias 16, para el diagnóstico
24 y para el tipo de intervención quirúrgica 36.
A
partir de la suma de los scores para
cada aspecto particular, se obtiene el
score de un paciente para cada etapa de tiempo t en que pertenece el paciente
en la UCIC. Este score determina finalmente la clasificación de la gravedad de
un paciente, etapa por etapa, en cualquiera de los siguientes estados: estado A
(bajo riesgo, score ≤ 25), estado B (riesgo medio, 26 ≤ score ≤ 41), estado C
(riesgo alto, 42 ≤ score ≤ 57), y estado D (riesgo grave, score ≥ 58).
Adicionalmente, a los estados anteriores se agrega un estado E, para indicar
que un paciente ya abandonó la UCIC en alguna etapa de tiempo.
Determinada la suma de los scores para cada aspecto en particular, se
obtiene el score de un paciente para
cada etapa de tiempo t en que
permanece en la UCIC (Unidad de Cuidados Intensivos Cardiología del Hospital
Dr. Luis Calvo Mackenna). El score determina a que estado tiene los siguientes
rangos:
Rango
|
Riesgo del paciente
|
||
Estado A
|
0
|
25
|
Bajo
|
Estado B
|
26
|
41
|
Medio
|
Estado C
|
42
|
57
|
Alto
|
Estado D
|
58
|
104
|
Grave
|
Adicionalmente, a los estados anteriores se agrega un
Estado E, para indicar que un paciente
ya abandonó la UCIC en alguna etapa de tiempo.
Dado a datos históricos se puede determinar el
comportamiento de un paciente a través del tiempo desde su ingreso a la UCIC
hasta que este sale o abandona dicha unidad.
Una vez definida la base de datos, se pretende determinar las
posibles secuencias de todos los ingresos a la UCIC, de este procedimiento
calculamos la probabilidades de tansicion Pij (en una etapa) dado
i=A,B,C,D,E y j= A,B,C,D,E
Las probabilidades pij
son obtenidas a partir de calcular el cociente entre la cantidad total de
transiciones desde el estado i al estado j y el total de dichas transiciones
que simplemente se inician en el estado i (en otras palabras lo que se está
calculando es la frecuencia relativa de las transiciones de los estados
partiendo del estado i), considerando
todas aquellas transiciones (en una etapa) que tengan lugar en cualquier etapa
del conjunto de secuencias (solo se podrá tener en cuenta las transiciones que
estén definidas para los estados). Adicionalmente, es de vital importancia
definir las probabilidades de transición para el estado E debido a que cuando
el paciente llega a este estado sale del sistema. Definimos las siguientes
probabilidades de transición para el estado E:
Ya definidas las probabilidades de transición, se podrá
observar el comportamiento que tendrá el paciente al ingresar a la UCIC en uno
cualquiera de los estados considerados por medio de la aplicación de la ecuación de chapman-kolmogorov (p(n) = p(n-1) *p)
a la matriz de transición generada por las probabilidades de transición de los
estados.
Resultados
En el estudio realizado por la UCIC se consideraron una
muestra de 64 ingresos diferentes, cuyos datos fueron registrados por un
periodo de 14 meses, es los cuales las estadías de los pacientes variaron entre
1 y 32 días de los cuales se obtuvo la información requerida para el
modelamiento de las cadenas de Markov. Para simplificar los cálculos realizados,
cada etapa de la Cadena de Markov corresponde a un periodo de dos días y los
datos considerados abarcan pacientes que estuvieron entre una y 16 etapas. Así
entonces, para cada uno de los 64 ingresos se calculó el score de cada paciente en cada etapa de su
permanencia, lo que determinó, a su vez, la secuencia de estados en el sistema.
De las 64 secuencias se obtuvo la siguiente matriz de probabilidades de
transición (en una etapa), cuyos elementos Pij corresponden a la probabilidad de pasar de un
estado i a un estado j al cabo de dos días:
Estas probabilidades de transición son debidas a que en
estado E es un estado absorbente (no
se puede salir de él), ya que este indica la salida de un paciente de la UCIC
por lo cual no puede llegar a estar en los riesgos definidos por los estado A, B,
C, D.
Ya definidas las probabilidades de transición, se podrá
observar el comportamiento que tendrá el paciente al ingresar a la UCIC en uno
cualquiera de los estados considerados por medio de la aplicación de la ecuación de chapman-kolmogorov (p(n) = p(n-1) *p)
a la matriz de transición generada por las probabilidades de transición de los
estados.
Observación: Esta matriz de transición
posee dos clases de estados, una clase de estados transigentes, formada por los
estados A, B, C y D, y una clase de estados recurrentes,
dada por el estado absorbente E. Además, la cadena posee una distribución
estacionaria (cuando las probabilidades de largo plazo
existen y son independiente
de la distribución inicial (f0)) que indica que con probabilidad 1 el
paciente hará abandono de la UCIC en el largo plazo.
A
partir de los datos de uno de los grupos se hicieron los cálculos anteriores
para obtener la estadía promedio estimada usando valores de n=1,2,…,16
etapas. Esto resultan de calcular
primeramente el número de veces que se visitó un determinado estado j en las n
etapas de toda la muestra de este grupo (considerando las secuencias truncadas
de hasta n etapas) dividido por el tamaño de la muestra, cuya posterior suma
tomando todos los valores posibles de j=A, B, C y D arroja la estadía
observada.
